Estimating NFL Team-Specific Home-Field Advantage

This morning, I tinkered a bit with my pro-football preseason team strength survey data from 2013 and 2014 to see what other simple things I might do to improve the accuracy of forecasts derived from future versions of them.

My first idea is to go beyond a generic estimate of home-field advantage—about 3 points, according to my and everyone else’s estimates—with team-specific versions of that quantity. The intuition is that some venues confer a bigger advantage than others. For example, I would guess that Denver enjoys a bigger home-field edge than most teams because their stadium is at high altitude. The Broncos live there, so they’re used to it, but visiting teams have to adapt, and that process supposedly takes about a day for every 1,000 feet over 3,000. Some venues are louder than others, and that noise is often dialed up when visiting teams would prefer some quiet. And so on.

To explore this idea, I’m using a simple hierarchical linear model to estimate team-specific intercepts after taking preseason estimates of relative team strength into account. The line of R code used to estimate the model requires the lme4 package and looks like this:

mod1 <- lmer(score.raw ~ wiki.diff + (1 | home_team), results)

Where

score.raw = home_score - visitor_score

wiki.diff = home_wiki - visitor_wiki

Those wiki vectors are the team strength scores estimated from preseason pairwise wiki surveys. The ‘results’ data frame includes scores for all regular and postseason games from those two years so far, courtesy of devstopfix’s NFL results repository on GitHub (here). Because the net game and strength scores are both ordered home to visitor, we can read those random intercepts for each home team as estimates of team-specific home advantage. There are probably other sources of team-specific bias in my data, so those estimates are going to be pretty noisy, because I think it’s a reasonable starting point.

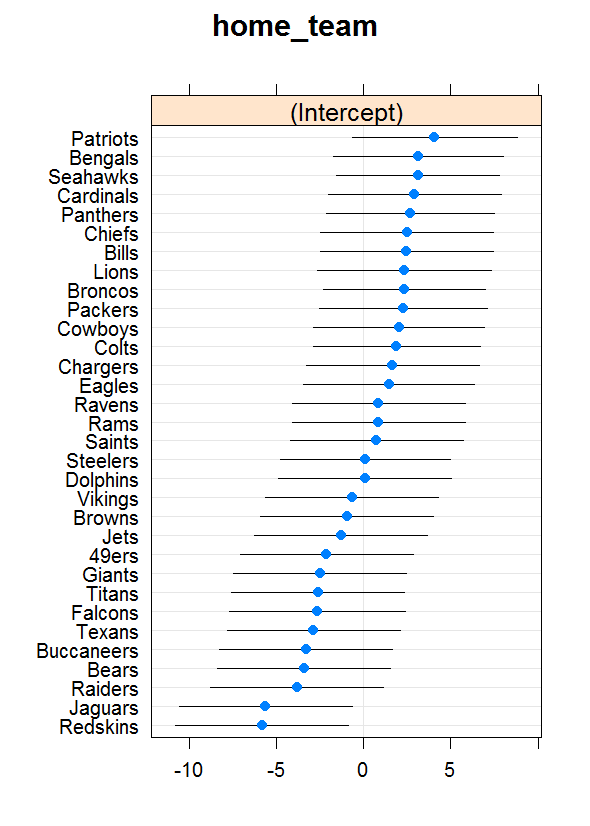
My initial results are shown in the plot below, which I get with these two lines of code, the second of which requires the lattice package:

ha1 <- ranef(mod1, condVar=TRUE)

dotplot(ha1)

Bear in mind that the generic (fixed) intercept is 2.7, so the estimated home-field advantage for each team is what’s shown in the plot plus that number. For example, these estimates imply that my Ravens enjoy a net advantage of about 3 points when they play in Baltimore, while their division-rival Bengals are closer to 6.

In light of DeflateGate, I guess I shouldn’t be surprised to see the Pats at the top of the chart, almost a whole point higher than the second-highest team. Maybe their insanely home low fumble rate has something to do with it.* I’m also heartened to see relatively high estimates for Denver, given the intuition that started this exercise, and Seattle, which I’ve heard said enjoys an unusually large home-field edge. At the same time, I honestly don’t know what to make of the exceptionally low estimates for DC and Jacksonville, who appear from these estimates to suffer a net home-field disadvantage. That strikes me as odd and undercuts my confidence in the results.

In any case, that’s how far my tinkering took me today. If I get really bored motivated, I might try re-estimating the model with just the 2013 data and then running the 2014 preseason survey scores through that model to generate “forecasts” that I can compare to the ones I got from the simple linear model with just the generic intercept (here). The point of the exercise was to try to get more accurate forecasts from simple models, and the only way to test that is to do it. I’m also trying to decide if I need to cross these team-specific effects with season-specific effects to try to control for differences across years in the biases in the wiki survey results when estimating these team-specific intercepts. But I’m not there yet.

* After I published this post, Michael Lopez helpfully pointed me toward a better take on the Patriots’ fumble rate (here), and Mo Patel observed that teams manage their own footballs on the road, too, so that particular tweak—if it really happened—wouldn’t have a home-field-specific effect.

8 Comments

by Jay Ulfelder on January 24, 2015 • Permalink

Posted in Forecasting, Misc.

Tagged Baltimore Ravens, football, RStats

Posted by Jay Ulfelder on January 24, 2015

https://dartthrowingchimp.wordpress.com/2015/01/24/estimating-nfl-team-specific-home-field-advantage/

8 Comments

Cyrus
/ January 24, 2015

I wonder if there are additional ways to model home-field advantage that also speak to the underlying mechanism at work. Just off the top of my head, change in altitude, temperature, and distance traveled for visitors all may impact the intensity of the home-field advantage. In particular, I think distance travelled will provide the greatest amount of variation and is perhaps theoretically the most compelling of those factors.

mod1 <- lmer(score.raw ~ wiki.diff + vist.dist + (1 | home_team), results)

where

vist_dist = aerial distance travelled by visiting team.

Reply
- dartthrowingchimp
  / January 24, 2015
  
  That would be fun to try.
  
  Reply
- dartthrowingchimp
  / January 25, 2015
  I just did a quick version of this and am seeing a weak effect that is hard to distinguish from generic home-field advantage.
  
  I used the geocode function in the ‘ggmap’ package to get geocoordinates for all stadium cities, then I used a simple function found here to calculate the great-circle distance between home and away towns in kilometers for each game from 2013 and 2014. When I added the log of that distance to the equation as a fixed effect, here’s what the estimates looked like:
  
  Estimate Std. Error t value (Intercept) -8.3907 8.2784 -1.014 wiki.diff 0.1254 0.0227 5.525 log(travel_distance) 1.2162 0.9052 1.344
  
  It looks like the distance measure and the intercept get conflated into one noisy measure of generic home-field advantage that points in the hypothesized direction but doesn’t clearly show an independent effect from game-specific travel distance. Meanwhile, the estimates for the home-team-specific intercepts were basically unchanged.
  Reply
- dartthrowingchimp
  / January 25, 2015
  Turns out those travel distances are normally distributed, so no need to log. Instead, I just divided by 1,000 to get something that’s easier to interpret:
  
  Estimate Std. Error t value (Intercept) 1.42776 1.63881 0.871 wiki.diff 0.12625 0.02269 5.565 I(travel_distance/1000) 0.11985 0.13344 0.898
  
  So this implies that every 1,000 km traveled by the visitor is worth about 0.1 additional points of home advantage, and we can’t be confident that it’s really not 0.
  Reply
  - Cyrus
    / January 25, 2015
    
    thanks for undertaking that, it was worth a try at least!
Nathan
/ January 27, 2015

Home field disadvantage for the Jaguars could be partially down to playing a “home” game in London for the 2013-2014 seasons? (32 and 14 point defeats) Being statistically illiterate I couldn’t even guess how much those two games would contribute to the final outcome.

Not a clue for Washington

Reply
- dartthrowingchimp
  / January 27, 2015
  
  Thanks for pointing that out about the Jaguars. With just two seasons’ worth of data here, those two games could be moving their average a chunk. If I rerun the analysis, I think I’ll exclude the overseas showcase games, which don’t really fit the data-generating process I have in mind.
  
  Reply
cemsers
/ January 29, 2015

http://informaticayredesfacil.blogspot.com/

Reply